算法学习笔记(2)树状数组【转】
树状数组(Binary Index Tree, BIT)也是很多OIer心中最简洁优美的数据结构之一。最简单的树状数组支持两种操作,时间复杂度均为 :
单点修改:更改数组中一个元素的值
区间查询:查询一个区间内所有元素的和
当然,树状数组能维护的不局限于加法,支持的操作也不止这两种,甚至有大佬能用树状数组实现平衡树,但这篇笔记不会深入讨论(因为我也还不是很懂hh)。
我们还是先来看一道模板题,来看看树状数组最基本的应用场景:
(HDU P1166)敌兵布阵
Problem Description
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
Input
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
(1) Add i j,i和j为正整数,表示第i个营地增加j个人(j不超过30)
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人(j不超过30);
(3)Query i j ,i和j为正整数,i<=j,表示询问第i到第j个营地的总人数;
(4)End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
Output
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
这个数据范围,直接模拟肯定会T,所以我们要使用数据结构来维护数组,树状数组可以说是其中最简洁的一种。我们来看看树状数组是怎么实现的。
树状数组的引入
回顾一下,我们说,我们要实现两种操作:单点修改和区间求和。对于普通数组而言,单点修改的时间复杂度是 ,但区间求和的时间复杂度是
。


当然,我们也可以用前缀和的方法维护这个数组,这样的话区间求和的时间复杂度就降到了,但是单点修改会影响后面所有的元素,时间复杂度是。
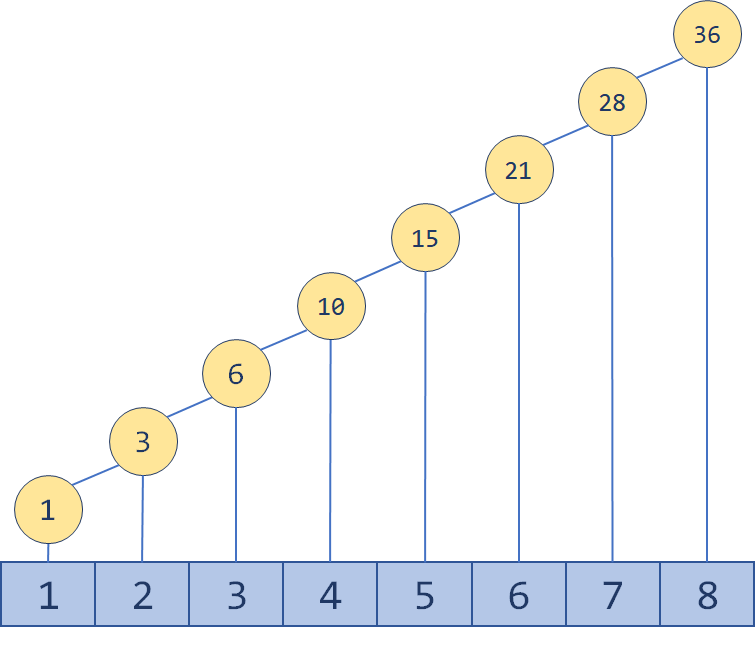
程序最后跑多长时间,是由最慢的一环决定的,因此现在我们希望找到这样一种折中的方法:无论单点修改还是区间查询,它都能不那么慢地完成。
注意到对 进行区间查询只需查询 和
然后相减即可(前缀和就是这样进行区间查询的),所以我们可以把区间查询问题转化为求前n项和的问题。
关于数组的维护,有个很自然的想法:可以用一个数组 维护若干个小区间,单点修改时,只更新包含这一元素的区间;求前n项和时,通过将区间进行组合,得到从1到n的区间,然后对所有用到的区间求和。实际上,设原数组是
,如果
维护的区间是
,此结构就相当于普通数组(还浪费了一倍内存);如果
维护的区间就是
,此结构就相当于前缀和。
现在我们试图寻找一种结构,一方面,单点修改时需要更新的区间不会太多;另一方面,区间查询时需要用来组合的区间也不会太多。
树状数组就是这样一种结构,它巧妙地利用了二进制(实际上,树状数组的英文名BIT,直译过来就是二进制下标树)。例如11,转化为二进制数就是 ,如果我们要求前11项和,可以分别查询
、
以及
的和再相加。这三个区间怎么来的呢?其实就是不断地去掉二进制数最右边的一个1的过程(如下图)。
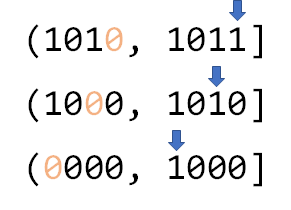

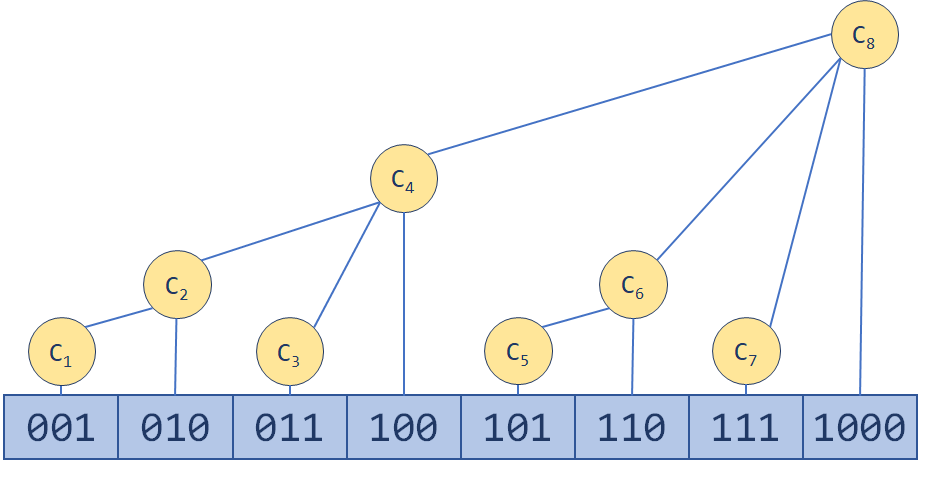
我们定义,二进制数最右边的一个1,连带着它之后的0为 (稍后再来看如何实现)。那么我们用 维护区间
,这样显然查询前n项和时需要合并的区间数是少于
的。树状数组的结构大概像下面这样:
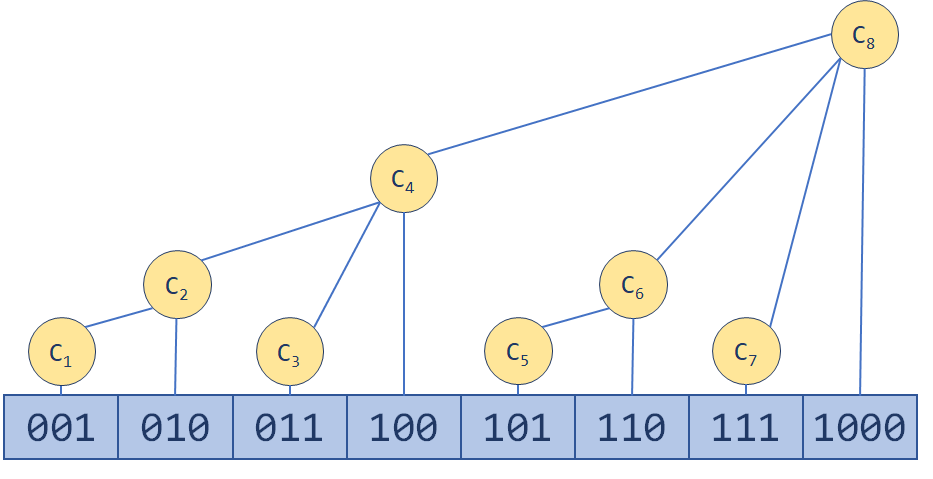
那么如何更新呢,大家会发现更新就是一个“爬树”的过程。一路往上更新,直到MAXN(树状数组的容量)。

我们举个例子来看看这树是怎么爬的。 现有二进制数 ,包含它的最小区间当然是。然后,它也肯定位于区间
内。然后是
,再然后是
……


如上图,每一步都把从右边起一系列连续的1变为0,再把这一系列1的前一位0变为1。这看起来像是一个进位的过程对吧?实际上,每一次加的正是 。(神奇吧?)这样,我们更新的区间数不会超过 。一个能以
时间复杂度进行单点修改和区间查询的数据结构就诞生了。
树状数组的实现
前面已经讲得很详细了,代码实现倒是一件简单的事了。不过我们需要先解决一个问题:lowbit怎么算?如果一位一位验证的话,会形成额外的时间开销。然而,我们有这样神奇的一个公式:
为什么可以这样?我们需要知道,计算机里有符号数一般是以补码的形式存储的。-x相当于x按位取反再加1,会把结尾处原来1000...的形式,变成0111...,再变成1000...;而前面每一位都与原来相反。这时我们再把它和x按位与,得到的结果便是lowbit(x)。下面的图中举了两个例子:


现在我们可以愉快地实现树状数组了:
单点修改
int tree[MAXN];
inline void update(int i, int x)
{
for (int pos = i; pos < MAXN; pos += lowbit(pos))
tree[pos] += x;
}求前n项和
inline int query(int n){
int ans = 0;
for (int pos = n; pos; pos -= lowbit(pos))
ans += tree[pos];
return ans;
}区间查询
inline int query(int a, int b){
return query(b) - query(a - 1);}初始化的时候,我们只需要update每个点的初始值即可。
树状数组的应用
还是先来看文章一开始那道题目的AC代码:
#include <cstdio>
#include <cstring>
#define MAXN 50005
#define lowbit(x) ((x) & (-x))int tree[MAXN];
inline void update(int i, int x){
for (int pos = i; pos < MAXN; pos += lowbit(pos))
tree[pos] += x;}
inline int query(int n){
int ans = 0;
for (int pos = n; pos; pos -= lowbit(pos))
ans += tree[pos];
return ans;}
inline int query(int a, int b){
return query(b) - query(a - 1);}int main(){
int cases;
scanf("%d", &cases);
for (int I = 1; I <= cases; ++I)
{
memset(tree, 0, sizeof(tree));
int n, x, a, b;
char opr[10];
printf("Case %d:\n", I);
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
{
scanf("%d", &x);
update(i, x);
}
while (scanf("%s", opr), opr[0] != 'E')
{
switch (opr[0])
{
case 'A':
scanf("%d%d", &a, &b);
update(a, b);
break;
case 'S':
scanf("%d%d", &a, &b);
update(a, -b);
break;
case 'Q':
scanf("%d%d", &a, &b);
printf("%d\n", query(a, b));
}
}
}
return 0;}然而,这只是树状数组最基本的应用。树状数组的应用是非常广泛的,例如,非常常见的一个应用是求逆序对:
(洛谷P1908) 逆序对
题目描述
猫猫TOM和小老鼠JERRY最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。最近,TOM老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中ai>aj且i<j的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
输入格式
第一行,一个数n,表示序列中有n个数。
第二行n个数,表示给定的序列。序列中每个数字不超过10^9
输出格式
给定序列中逆序对的数目。
当然逆序对也可以用归并排序的方法求,但树状数组的空间复杂度更低。其实我们与其说在用树状数组求逆序对,不如说是在求非严格顺序对(顺序对和相等对),然后间接算出逆序对的数量。我们是怎么算出非严格顺序对的个数的呢?
例如,我们要求5 4 1 3 2的逆序对。用ans记录非严格顺序对的数量。
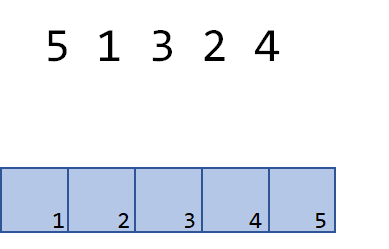
我们按顺序去填充树状数组,第一个数字是5,这时没有数比5小,所以ans保持为0。我们把tree[5]填为1。
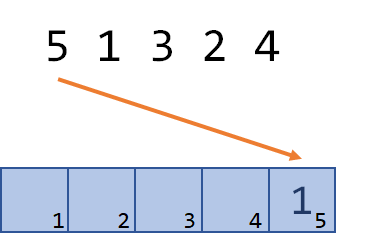
下一个数字是1,这时也没有数比1小,ans仍为0。我们把tree[1]填为1。
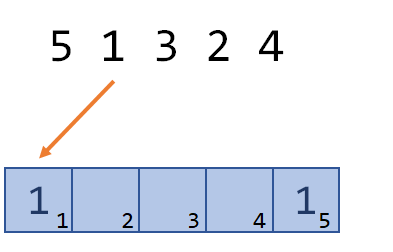
下一个数字是3,这时query(3)为1,有一个数比3小了,ans变为1。然后再填tree[3]。

下一个数字是2,这时query(2)为1,说明前面有一个数比2小,ans再加1变为2。然后填tree[2]。

最后一个数字是4,query(4)为3,说明前面有3个数比4小,ans加3变为5。所以非严格顺序对的总数就是5。那么逆序对共有 个。
当然,这道逆序对的题还涉及到离散化等问题,这个以后可能我也会写相关笔记。完整代码如下:
#include <cstdio>
#include <cctype>
#include <algorithm>
#define lowbit(x) ((x) & (-x))
#define MAXN 500010using namespace std;typedef long long ll;ll read() //快速读入,不是这篇文章的重点{
ll ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c))
{
ans = ans * 10 + c - '0';
c = getchar();
}
return ans;}ll tree[MAXN];inline void update(ll i, ll x){
for (ll pos = i; pos < MAXN; pos += lowbit(pos))
tree[pos] += x;}inline ll query(int n){
ll ans = 0;
for (ll pos = n; pos; pos -= lowbit(pos))
ans += tree[pos];
return ans;}inline ll query(ll x, ll y){
return query(y) - query(x - 1);}int A[MAXN]; //离散化后的数组typedef struct{
ll value, id;} mypair;mypair B[MAXN]; //原始数组(同时存储id)bool cmp(mypair x, mypair y){
if (x.value < y.value)
return true;
else if (x.value == y.value && x.id < y.id)
return true;
return false;}int main(){
ll n = read(), sum = 0;
for (int i = 1; i <= n; i++)
{
B[i].value = read();
B[i].id = i;
}
sort(B + 1, B + n + 1, cmp);
for (int i = 1; i <= n; i++)
A[B[i].id] = i;
for (int i = 1; i <= n; i++)
{
sum += query(A[i]);
update(A[i], 1);
}
sum = n * (n - 1) / 2 - sum;
printf("%lld\n", sum);
return 0;}这里面还写了一个快速读入,可以不必太在意,重点还是在于这段代码:
for (int i = 1; i <= n; i++){
sum += query(A[i]);
update(A[i], 1);}其实单单是对这个求逆序对的拓展应用,就有不少题目了,可见这个树状数组的应用面是多么广泛。但这篇文章已经很长了(我水平也有限),就先写到这儿吧。
2 条评论
发表评论